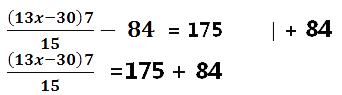(I) W literaturze anglosaskiej transpozycja, w literaturze polskiej przekształcenie tożsamościowe
(II) Równanie
, jest nietrywialną postacią równania ax + b = 0
(w odróżnieniu od jego postaci trywialnej, np. 2x + 3 = 0). Jego rozwiązaniem jest liczba x = 45. Rozwiązywanie należy rozpocząć od podzielenia obydwu stron równania przez liczbę 1225 (dlaczego?), a czytelnicy zapewne wskażą jeszcze pozornie inne procedury prowadzące do sukcesu. Zachęcamy do jego rozwiązania, gdyż ten proces najpełniej uzmysłowi czytelnikowi, jakim wyzwaniem w edukacji matematycznej dzieci i młodzieży jest wyjaśnienie problemu: dlaczego tak, a nie inaczej transponuje się równania, aby uzyskać rozwiązanie. Rozwiązanie akurat tego problemu wymaga użycia jedynie najbardziej elementarnych narzędzi szkolnej arytmetyki: odejmowanie, mnożenie, dzielenie, ułamek, nawias, odwrotność liczby!
(III) Równanie postaci
jeszcze 20 lat temu, było w Polsce jednym z pięciu, typowych zadań, z których składał się egzamin do szkoły średniej – czas rozwiązania ok. 15 minut, bez użycia kalkulatora. Szacowanie dokonane zostało na podstawie badań własnych autora oraz analizie statystycznej wyników egzaminów maturalnych Centralnej Komisji Egzaminacyjnej polskiego Ministerstwa Edukacji Narodowej, zamieszczonych na oficjalnej stronie internetowej
I. Prawdy naukowe: twórczość czy odkrywanie
Naukowców od stuleci(IV) absorbuje poszukiwanie odpowiedzi na pytanie:
„Matematyka (a szerzej, również prawdy naukowe) istnieje i jest jedynie odkrywana, czy też jest ona wyłącznie wytworem oryginalnej twórczości poszczególnych badaczy ?”
(IV) Literatura przedmiotu, np. w (1) zaczyna na ogół od postaci Pitagorasa(„świat jest liczbą”) i Platona - jako prekursorów tego sposobu myślenia o matematyce. Należy zwrócić jednak uwagę na brak wiarygodnych, z punktu widzenia metodologii badań naukowych, źródeł dotyczących starożytności. Polski badacz, M. Kordos w (2) uzasadnia następująco konieczność bardziej krytycznego traktowania hipotez dotyczących starożytności, cyt.: „[…]Ponoć pierwszym dyrektorem tej biblioteki ( chodzi o bibliotekę w Aleksandrii, przyp. autora) został Euklides. Jest zdumiewające, jak mało o nim wiemy. Pisze się, że był z Megary (ale to w wyniku pomylenia go z innym Euklidesem), podaje się daty jego życia (przeważnie 365 – 300 p.n.e.), twierdzi się, że odbył studia w Akademii Platońskiej (no, bo każdy szanujący się uczony tych czasów…), że miał znaczące wykształcenie w zakresie starożytnej (już wówczas) wiedzy egipskiej (bo Aleksandria leży w Egipcie) itd. Wszelkie jednak próby potwierdzenia którejkolwiek z tych informacji choćby z dwóch źródeł kończą się niepowodzeniem.” Przyp. autora
Konsekwencją wyboru tylko jednego rodzaju podejścia, co do sposobu uprawiania nie tylko matematyki, ale i nauki w ogóle, może być
inercja heurystyczna(V):niemożność dokonywania pewnych fundamentalnych odkryć.
(V) Istotne znaczenie pojęciu heurystyki nadał w (3) wybitny matematyk amerykański George Polya, uważając, że przynajmniej w odniesieniu do matematyki, umiejętność dokonywania odkryć naukowych można kształcić, i to już od najmłodszych lat. Przyp. autora
W prezentowanym poniżej doniesieniu naukowym dotyczy to na przykład
twierdzenia o algorytmie(VI) znajdowania rozwiązania równania liniowego – zagadnienia o znaczeniu fundamentalnym swoją rangą dla nauki i edukacji(VII)
(VI, VII) Pojęcie algorytmu w artykule odnosi się do sformułowania, uzasadnionej metodologią naukową, listy kroków niezbędnych i wystarczających do uzyskania rozwiązania równania
z jedną niewiadomą. Jest rzeczą zdumiewającą, że umiejętność posługiwania się jednym z najistotniejszych narzędzi nie tylko matematyki, ale i nauki w ogóle, jakim jest równanie z jedną niewiadomą, w edukacji szkolnej musi być, z uwagi na brak takiego algorytmu, wykształcone intuicyjnie. Tym samym jest relatywnie czasochłonne i rozłożone na bardzo wiele lat. Na przykład w szkole polskiej z równaniami liniowymi dzieci stykają się już w wieku lat 6 rozwiązując problemy w rodzaju: 1+ ? = 3, a kończą po kolejnych 12 latach nauki, rozwiązywaniem równań liniowych zapisanych w postaci wymiernej: a = - b/x ! Intuicyjne wykształcenie, szkolnych kompetencji matematycznych, skutkuje u ludzi bardzo szybkim ich wyparciem z pamięci. R. Feyneman komentował ten stan rzeczy następująco: „Jest coś niedobrego z ludźmi: nie uczą się przez zrozumienie, tylko jakoś inaczej, pewnie z pamięci. Ich wiedza jest taka krucha”. Z przeprowadzonych przez autora badań w Polsce, wynika, że większość absolwentów szkół średnich po 20 latach potrafi wskazać algorytm rozwiązywania równań kwadratowych w trywialnej postaci uporządkowanej: ax2+bx+c = 0 („[…]trzeba obliczyć Δ=b2-4ac oraz x1 i x2”),natomiast nie potrafi przekształcić wzoru, a więc i uporządkować równania do trywialnej postaci ogólnej – oczywistej do rozwiązania. W szkolnej edukacji matematycznej, równania występują właściwie wyłącznie w postaci nieuporządkowanej (nietrywialnej), przede wszystkim dlatego, by wykształcić elementarną umiejętność przekształcania wzorów i algebraiczną biegłość w przekształceniach.
Historia matematyki pokazuje, że jedynie w przypadku trywialnej postaci ogólnej równań liniowych i kwadratowych (równań stopnia drugiego) udało się częściowo taki elegancki algorytm sformułować. Fragmentaryczność procedury rozwiązywania tych równań jest zdeterminowana koniecznością ich występowania w trywialnej postaci uporządkowanej – równania stopnia 1, jako ax+b = 0 (rozwiązanie ma postać x = - b/a. Warto jednak podkreślić, że kolejność niezbędnych transpozycji nie ma w tym wypadku znaczenia, a tym samym nawet w rozwiązywaniu równań liniowych w postaci trywialnej nie potrafimy uzasadnić dlaczego wykonujemy określoną transpozycję: można najpierw dzielić, a potem odejmować i odwrotnie, najpierw wykonać odejmowanie, a w kroku następnym rozwiązania – dzielenie. Wynik będzie taki sam!). Rozwiązanie równania stopnia 2, gdy jest ono uporządkowane do trywialnej postaci ogólnej: ax2+bx+c = 0, może dawać odpowiednio: jedno lub dwa rozwiązania, bądź ich nie posiadać. Dzięki wynikom Galois i Abela wykazano nawet, że metoda ogólna dla równań stopnia 5 i wyższych - nawet dla trywialnych postaci ich zapisu - nie istnieje, a procedury porządkowania równań wielomianowych wszystkich stopni do trywialnej postaci ogólnej: axn+bxn-1+…+ c = 0 nie wypracowano. O ile w przypadku tych ostatnich dotyczy to zainteresowań wąskich grup specjalistów, to w przypadku algorytmu porządkowania równań liniowych oraz równań stopnia 2 do trywialnej postaci ogólnej – oczywistej dla wskazania rozwiązania- kwestia jest fundamentalną dla edukacji, a tym samym dla kształcenia przyszłych naukowców, wreszcie jak to ujął C. F. Gauss dla „powagi samej matematyki”. Bez umiejętności porządkowania równań do postaci trywialnej, a tym samym rozwiązywania tych równań, nawet jeżeli czyni się to tak jak dotychczas – czyli intuicyjnie – z uwagi na matematyzację życia codziennego, uprawianie nauki, nawet w zakresie odtwórczym, jest niemożliwe. Wiele dyscyplin naukowych, nie tylko matematycznych jak np. Algebra, nie mogłoby powstać. Z kolei edukacja matematyczna bez tej umiejętności, na poziomie rozumienia problemu, musiałaby się kończyć co najwyżej na dodawaniu, mnożeniu, potęgowaniu, odejmowaniu, dzieleniu i pierwiastkowaniu. Dlaczego? Twierdzenie o znajdowaniu rozwiązania równania liniowego (a tym samym umiejętność przekształcania wzorów) jest uprzednie w stosunku do twierdzenia Talesa, Pitagorasa i pozostałych narzędzi matematyki ! Tym samym, bez jego znajomości i umiejętności posługiwania się tym twierdzeniem, chociażby intuicyjnie, jak dotychczas, nie mogłoby mieć miejsca nauczanie nie tylko geometrii, algebry, logarytmów czy też trygonometrii, ale także nauczanie fizyki, chemii i rozwiązywanie wielu elementarnie istotnych zagadnień technicznych. Przyp. autora.
Zauważmy, że inne, niż postulowane logiką zero – jedynkowe podejście, pozwala na uprawianie nauki także w sposób następujący: prawdy naukowe istnieją, ale ich odkrywanie jest konsekwencją oryginalnych aktów twórczych
i badań naukowych, w sposób często istotnie niezależny od rozstrzygnięć dotyczących istnienia tychże prawd.
II. Twierdzenie o algorytmie uzyskiwania rozwiązania równania liniowego postaci: ax + b = 0
Pitagorejskie podejście do nauki: „Świat jest liczbą” (w domyśle: matematyką) prawdopodobnie zaciążyło nad problemem, następującym podejściem: „równania istnieją, a ludzkość je jedynie odkrywa”. To z kolei przyniosło w konsekwencji ograniczenie – wspomnianą wyżej zdumiewającą inercję heurystyczną. Jakkolwiek wielu historyków nauki skłania się ku poglądowi pierwszeństwa Hindusów w rozwiązywaniu równań(VIII), to dokonania arabskich uczonych w tym zakresie, sprzed ponad tysiąca lat, dały zarówno matematyce, jak i nauce w ogóle, impuls rozwojowy, którego rangi nie sposób przecenić.
(VIII) A.P. Juszkiewicz w (4) pokazuje osiągnięcia matematyki hinduskiej i arabskiej w tej dziedzinie, a w (5) G. Ifrah wręcz wskazuje na zawłaszczenie tych osiągnięć przez historyków matematyki z innych kręgów kulturowych – upominając się o przywrócenie właściwych proporcji w relacjonowaniu zagadnienia.
Przez stulecia sformułowano i wykazano trywialną postać rozwiązania równania liniowego ax + b = 0: x = - b/a , wskazano narzędzia , którymi trzeba się posłużyć, aby to rozwiązanie uzyskać – metoda transpozycji(IX) w literaturze anglosaskiej – natomiast nikt nie potrafił(?) nie próbował(?) wskazać algorytmu rozwiązywania tych równań, gdy występują w postaci nieuporządkowanej (nietrywialnej ) tak, jak np. wspomniane już równanie: - a to właśnie na takich problemach kształci się umiejętność rozwiązywania równań i przekształcania wzorów z fizyki, chemii etc. przy okazji szkolnej edukacji. Tym samym nie można było pokazać rozwiązania fundamentalnego dla matematyki problemu(X) : w jakiej kolejności (i ilu!) należy (i wystarczy!) dokonać przekształceń tożsamościowych (transpozycji) w celu uzyskania trywialnej, a więc i oczywistej do rozwiązania postaci ogólnej, najprostszego typu równania, jakim jest równanie liniowe postaci: ax + b = 0.
(IX, X) A.P. Juszkiewicz w (4) pokazuje osiągnięcia matematyki hinduskiej i arabskiej w tej dziedzinie, a w (5) G. Ifrah wręcz wskazuje na zawłaszczenie tych osiągnięć przez historyków matematyki z innych kręgów kulturowych – upominając się o przywrócenie właściwych proporcji w relacjonowaniu zagadnienia.
W pewnym uproszczeniu można stwierdzić, że wspomniane podejście, skutkuje w praktyce naukowej i edukacyjnej, jedynie kombinacyjno-intuicyjną umiejętnością rozwiązywania równań liniowych, których zapis występuje w postaci nietrywialnej. Nawet najwybitniejsi matematycy (naukowcy) rozwiązują równania liniowe wg zasady: „ dokonuję takiej, a nie innej transpozycji w równaniu, nie dlatego, że znam regułę rządzącą kolejnością niezbędnych kroków w celu znalezienia rozwiązania, ale dlatego, że tak się to robi”.
Taka sytuacja prowadzi do upokarzającej sytuacji: na pytanie ucznia, dlaczego dokonujemy takiej, a nie innej transpozycji, standardowa odpowiedź musi brzmieć: bo tak się robi w matematyce!!! W matematyce, która w stopniu najwyższym – bo z założenia – szczyci się dedukcyjnością swej dyscypliny, przez powiązanie skutku z przyczyną.
Nauczyciel matematyki w szkole dysponuje jedynie własną intuicją rozwiązywania równań. Jego zadanie to wykształcenie takiej intuicji uczniom, co przy powszechności nauczania musi implikować równie powszechne problemy. Zmiana podejścia: matematykę (naukę) badacze tworzą, niezależnie od jej istnienia, pozwala na sformułowanie reguły, która daje matematykom, uczniom i studentom oręż w postaci pewnika wyboru konkretnej transpozycji w równaniu:
Twierdzenie: „Dokonując przekształceń tożsamościowych ( transpozycji) na liczbie (a) przyrównanej do litery (x), czyli: x = a, możemy utworzyć dowolne równanie, które ma jedno rozwiązanie.(XI) Odwrócenie w kolejności tych operacji daje równość wyjściową. Transpozycje prowadzące do rozwiązania równania wykonuje się, rugując zbędne czynniki, w kolejności odwrotnej do reguły kolejności wykonywania działań arytmetycznych, działaniami przeciwnymi:
- Czynnik występujący w sumie rugujemy transpozycją odejmowania
- Czynnik występujący w różnicy rugujemy transpozycją dodawania
- Czynnik występujący w iloczynie rugujemy transpozycją dzielenia
- Czynnik występujący w mianowniku ilorazu rugujemy transpozycją
mnożenia.
- Czynnik występujący w potędze o wykładniku -1 (odwrotność) rugujemy transpozycją podniesienia obydwu stron równania również do potęgi o wykładniku -1.
(XI) W celu uniknięcia zbędnych dygresji dokonuje się następującego zastrzeżenia: przedmiotem artykułu są równania z jedną niewiadomą (x) występującą w pierwszej potędze, która w równaniu może występować wielokrotnie. Z kolei samo konstruowanie równań nie jest zabiegiem nowatorskim. W (5) A.P. Juszkiewicz wspomina o wielu hinduskich uczonych, którzy opisywali procedurę układania równania do konkretnego zadania, a następnie podawali regułę jego rozwiązywania (Prtudakaswami, BhaskaraII, Narajana). A.P. Juszkiewicz podkreśla podobieństwo ich metod do, cyt.: „szczegółowego przepisu na „układanie równań przy rozwiązywaniu zadań”, który prawie tysiąc lat później podał R. Descartes w swojej Geometrii (1637).” W konsekwencji, przeprowadzone rozumowania, nie prowadziły jednak do sformułowania zasady ogólnej, skutkującej udowodnionym twierdzeniem. Stąd i jego brak w podręcznikach. Przyp. autora.
Dla ilustracji efektywności dydaktycznej przedstawionego algorytmu, wymuszającego pułap rozumienia problemu, rozważmy podane twierdzenie na konkretnym przykładzie:
-
Przyrównujemy dowolną liczbę rzeczywistą a do litery x i otrzymujemy równość:
- Na mocy twierdzeń o dokonywaniu transpozycji w równaniach liniowych możemy do obydwu stron równości np. dodać dowolną liczbę rzeczywistą b (np. dodać liczbę 3), a następnie pomnożyć obydwie strony równania przez dowolna liczbę rzeczywistą c (np. pomnożyć przez liczbę 4):
| x = a │ +b | x = 2 │ +3 |
| x + b = a + b │ • c | x + 3 = 5 │• 4 |
| c∙(x + b) = c∙(a + b) | 4∙(x+3) = 20 |
- Wykonując operacje transpozycji na obydwu stronach utworzonego równania w odwrotnej kolejności (czyli rugując zbędne czynniki w kolejności odwrotnej do reguł kolejności wykonywania działań arytmetycznych) otrzymujemy wyjściowe przyrównanie liczby a do litery x, a więc rozwiązanie równania (czyli przyrównania liczby 2 do litery x):
| c∙(x + b) = c∙(a + b) │: c | 4∙(x+3)= 20 │:4 |
| x + b = a + b │ – b | x + 3 = 5 │– 3 |
| x = a | x = 2 |
Nasuwa się pytanie, dlaczego, z uwagi na oczywistość i elementarną prostotę, przytoczone twierdzenie nie zostało dotychczas sformułowane? Odpowiedź wiąże się zapewne m.in. z rygoryzmem metod, którymi matematycy się posługują, uprawiając swoją naukę. Otóż kiedy w matematyce zostaje sformułowane nowe twierdzenie, to do zakwestionowania jego słuszności wystarczy, na ogół, podanie kontrprzykładu. Czasami formułuje się więc nowe twierdzenie, które uważa się za prawdziwe z dokładnością do wyjątku dla podanego kontrprzykładu, o ile jest to oczywiście dopuszczalne. Jeżeli jednak kontrprzykładów jest więcej to twierdzenie zostaje niejako „poddane”. Z oczywistych względów z większą uwagą atakowane jest twierdzenie, a nie kontrprzykład.
Podane, w części III artykułu omówienie zaproponowanego stosowania algorytmu w praktyce szkolnej, we wszystkich możliwych ( i istotnych z punktu widzenia dydaktyki zagadnienia) postaciach zapisu równań liniowych, pokazuje również falsyfikację kontrprzykładów. W tym miejscu omówiony zostanie najbardziej chyba spektakularny.
Dziecko uczestniczące w procesie szkolnej edukacji matematycznej, już na bardzo wczesnym jej etapie, dowiaduje się, że takie równanie rozwiązuje się następująco:
Musimy się godzić z sytuacją, w której uczeń, na pytanie: dlaczego dokonujemy właśnie takich transpozycji, może uzyskać jedynie odpowiedź: no bo tak się umówiono w matematyce, etc.
W równaniu ax+b=0,x≠ 0 dokonajmy następujących transpozycji:
Otrzymujemy równanie, którego zapis w postaci wymiernej zdaje się przeczyć podanemu wyżej twierdzeniu. Zauważmy jednak, że jest to jedynie formalnie inny (tożsamościowy), a nie faktycznie różny, sposób zapisania równania:
Przy takim zapisie równania poprawność twierdzenia jest w oczywisty sposób trywialna. Ponieważ o prawdziwości twierdzenia nie decyduje postać zapisu dowodzimy falsyfikacji kontrprzykładu:
Zgodnie z twierdzeniem, transpozycji rugowania zbędnych czynników dokonujemy
w kolejności odwrotnej do reguły kolejności wykonywania działań arytmetycznych, rugując zbędny czynnik działaniem przeciwnym do działania, w którym ten czynnik występuje. Czynniki zbędne występują w potęgowaniu i mnożeniu. W mnożeniu jest to liczba „-b”, dlatego rugujemy ją działaniem przeciwnym do mnożenia, dzieląc obydwie strony równania prze liczbę „-b”.
Czynnikiem zbędnym jest ujemny wykładnik w potędze liczby „x” (odwrotność liczby „x”). Działaniem przeciwnym jest podniesienie obydwu stron równania do potęgi „-1” .
Przegląd porównawczy algorytmów znajdowania rozwiązań równań
stopnia pierwszego
Matematyzacja nauki, a tym samym badań i odkryć naukowych, obliguje badaczy wszystkich dyscyplin naukowych, nawet tych bardzo odległych swoimi zainteresowaniami naukowymi od matematyki, do swobodnego posługiwania się równaniami liniowymi i wzorami z jedną niewidomą, z uwagi na linearność bardzo wielu zjawisk, których opisem zajmuje się nauka. Trudno oczekiwać by naukowiec zajmujący się np. naukami społecznymi, potrafił dostrzec i zapisać zależność linearną – równaniem, jeżeli nie potrafi takich równań swobodnie rozwiązywać
Umiejętność ta, czyli wyćwiczenie pokazanego w artykule algorytmu, stanowi także cezurę w nauce szkolnej matematyki. Dziecko w szkole, skazane jest w tym aspekcie nauczania matematyki, na intuicję nauczyciela, który, jak to pokazaliśmy powyżej, sam rozwiązuje równania intuicyjnie. Problemy dotyczące nauczania matematyki, obok sfery dotyczącej relacjonowania faktów, mają swoje źródło znacznie bardziej w konieczności kształcenia intuicji niż w ograniczeniach intelektualnych dziecka, określanych jako brak uzdolnień matematycznych(XII).
(XII) Niezwykle istotnym aspektem nauczania szkolnej matematyki jest właściwe zredefiniowanie formalizmów matematycznych na język zrozumiały dla uczniów i studentów, co postulował już A. Einstein: „należy upraszczać wszystko, co się da, nie bardziej jednak niż jest to potrzebne.” Przyp. autora
Zanim przejdziemy do przeglądu wszystkich istotnych w szkolnej edukacji postaci równań: ax + b = 0, rozwiążmy nasze tytułowe równanie:
Jak łatwo zauważyć jest ono równoważne zapisowi:
Rugujemy zbędny czynnik – liczbę 1225 – występujący w mnożeniu, transpozycją dzielenia:
Rugujemy zbędny czynnik – wykładnik -1 – transpozycją jest podniesienie obydwu stron równania do potęgi (…)-1
Rugujemy zbędny czynniki – liczbę 84 w odejmowaniu – transpozycją jest dodanie do obydwu stron równania liczby 84:
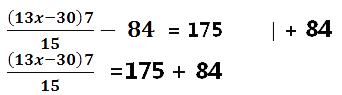
Rugujemy zbędny czynnik – liczbę 15 w ilorazie – transpozycją jest pomnożenie obydwu stron równania przez liczbę 15
Rugujemy zbędny czynnik – liczbę 7 w iloczynie – transpozycją jest podzielenie obydwu stron równania przez liczbę 7
Rugujemy zbędny czynnik – liczbę 30 w różnicy – transpozycją jest dodanie do obydwu stron równania liczby 30
Rugujemy zbędny czynnik – liczbę 13 w iloczynie – transpozycją jest podzielenie obydwu stron równania przez liczbę 13
Kształcenie umiejętności rozwiązywania równań przez ich budowanie, umożliwia w procesie edukacji matematycznej, rozumienie sensu kolejnych transpozycji. Staranne przestudiowanie z dzieckiem tego jednego równania, poprzez jego stopniowe rozszerzanie o kolejne transpozycje pozwala na szybkie wykształcenie umiejętności swobodnego rozwiązywania wszystkich równań. Są dwa przypadki szczególne: niewiadoma występuje więcej niż jeden raz po tej samej stronie równania oraz niewiadoma występująca więcej niż jeden raz po obydwu stronach równania, które omawiamy w artykule poniżej.
Algorytm uzyskiwania rozwiązania równania liniowego
Otrzymanie istotnego rezultatu w matematyce elementarnej powszechnie uchodzi za rzecz niemożliwą. Dzieje się tak z uwagi na to, że matematyka jest właściwie jedyną dyscypliną naukową, w której raz udowodniony fakt pozostaje niepodważalną prawdą naukową, aż po kres jej istnienia. Jednak okazuje się, że nawet „królowa nauk” zawiera pewne przeoczenia. Są one związane ze sposobem przekazywania wiedzy, utrwalonym przez tysiąclecia tradycją i szkolną rutyną. Co najbardziej intrygujące, to fakt iż dotyczy to najważniejszego narzędzia badawczego matematyki – jakim jest od jej zarania równanie liniowe. Literatura przedmiotu np. w (6,7) podaje jedynie narzędzia, jakich można użyć w celu uzyskania rozwiązania równania liniowego, natomiast nie podaje kolejności w jakiej należy to uczynić. Można jedynie snuć domysły dlaczego przez trzy tysiąclecia posługiwania się równaniami liniowymi, problem tej rangi umknął uwadze matematyków. W praktyce bowiem, brak pewnika wyboru właściwej transpozycji równania, nie pozwala na jednojednoznaczne określenie procedury rozwiązywania równań: co i w jakiej kolejności wykonać aby zawsze algorytm prowadził do sukcesu.
Na ogół (np.w6,7) problem omawia się następująco:
- Równanie liniowe to równanie, w którym niewiadoma x występuje jedynie W potędze o wykładniku 0 lub 1 i ma postać: ax+b=0
- Rozwiązanie równania liniowego ma postać: x = – b/a
- Rozwiązanie równania liniowego uzyskujemy metodą transpozycji (w litera- turze polskiej met. równań tożsamość.) na podstawie następujących twierdzeń:
I. Każde równanie liniowe można przekształcić tożsamościowo w równoważne mu równanie
II. Do obydwu stron równania można dodać tą samą liczbę
III. Od obydwu stron równania można odjąć tą samą liczbę
IV. Obydwie strony równania można pomnożyć przez tą samą liczbę, różną od zera
V. Obydwie strony równania można podzielić przez tą sama liczbę, różną od zera.
Powyższe twierdzenia nie pokazują minimalnej liczby kroków i ich kolejności, gwarantujących sukces jakim jest osiągnięcie rozwiązania.
Brak takiego jednojednoznacznego algorytmu opisującego kolejność koniecznych do wykonania kroków w celu osiągnięcia rozwiązania równania - liniowego to doprawdy jedno z najbardziej zdumiewających przeoczeń w historii nauki, a w historii matematyki i jej dydaktyki w szczególności . W podręcznikach w miejsce postulowanego w tym artykule twierdzenia, podaje się jedynie kilka, przykładowo rozwiązanych, typowych równań i… następuje przejście do ćwiczeń. Jeżeli profesjonalni matematycy ( a więc i nauczyciele matematyki) nie dysponowali algorytmem pokazanym w tym artykule, a jedynie wypracowywali w sobie jego nienazwaną intuicję, to trudno oczekiwać by potrafili w sposób przekonywujący objaśnić zagadnienie. W dydaktyce matematyki na poziomie elementarnym jest to rozstrzygający moment dla przyswajania kolejnych treści i rozwiązywania problemów nie tylko matematycznych, ale również tych z zakresu szkolnej fizyki czy też chemii: „pojmij albo giń”. Brak twierdzenia: „Rozwiązanie równania liniowego znajdujemy metodą transpozycji, pozbywając się zbędnych czynników w kolejności odwrotnej do kolejności wykonywania działań arytmetycznych”
i dokonania systematycznego przeglądu sposobu osiągania rozwiązania wszystkich postaci równań liniowych, jest jedną z fundamentalnych przyczyn niskiego poziomu edukacji matematycznej i postrzeganiem tego przedmiotu jako niezwykle trudnego. Wystarczy, że uczeń wyposażony w powyższe twierdzenie, będzie przestrzegał powtarzania zaprezentowanej poniżej procedury dwóch kroków - zawsze osiągnie sukces. Procedura w kroku pierwszym wymaga dokonania przeglądu występujących w równaniu działań arytmetycznych i wskazania działania głównego – czyli tego, które jest do wykonania jako ostatnie z uwagi na kolejność wykonywania działań arytmetycznych. Krok drugi to wykonanie na obydwu stronach działania przeciwnego do działania głównego, co pozwala na wyrugowanie z równania tej części działania głównego, w której nie występuje niewiadoma. Powtarzanie tej procedury dwóch kroków zawsze gwarantuje sukces w najmniejszej liczbie transpozycji. Pokażemy tą procedurę na następującym przykładzie:
| ax + b = c , x=? | 1. Mamy dwa działania: mnożenie i dodawanie. Ostanie w kolejności wykonywania działań ( czyli +) nazywamy działaniem głównym. |
| ax + b = c | -b | 2.Pozbywamy się tej części działania głównego, w której nie występuje poszukiwana niewiadoma, działając na obydwie strony równania działaniem przeciwnym do działania głównego, czyli od obydwu stron równania odejmujemy b |
| ax = c – b | |
Powtarzamy procedurę:
| ax = c – b | 1. Wskazujemy działanie główne: mnożenie (•) |
| ax = c – b |:a | 2. Pozbywamy się tej części działania głównego, w której nie występuje poszukiwana niewiadoma, działając na obydwie strony równania działaniem przeciwnym do działania głównego, czyli obydwie strony równania dzielimy przez a
|
 | |
Jak łatwo zauważyć do stosowania tej procedury wystarcza przytoczone twierdzenie i znajomość kolejności wykonywania działań arytmetycznych. Przystępność tej procedury, czyni zagadnienie zarówno łatwym i intuicyjnie logicznym, tak dla zrozumienia jak i objaśnienia. Oczywistym jest również dowód tego twierdzenia, który odwraca tradycyjne podejście od postaci równania do jego rozwiązania – zakładamy, że rozwiązanie równania jest pierwotne, a jego postać jest następstwem działań arytmetycznych na obydwu stronach rozwiązania. Budując pojęciowy model fizyczny dla ucznia, możemy pokazywać, że postać równania jest zaszyfrowanym rozwiązaniem, które powstało w następujący sposób:
- Zakładamy, że istniejącemu rozwiązaniu x jest przyporządkowana konkretna wartość liczbowa:
- Postulujemy uzyskanie jakiejś dowolnej postaci równania liniowego, np.:
- Określamy kolejność wykonywania działań w postulowanej strukturze: mnożenie przez liczbę a i dodawanie liczby b oraz wykonujemy ją na x = k:
| x = k | • a | x = 2 | • 6 |
| ax = ak | + b | 6x = 2 • 6 | + 1 |
| ax + b = ak + b = c | 6x + 1 = 2 • 6 + 1= 13 |
- Odwracając procedurę uzyskujemy x = k i x = 2 przeprowadzając przystępny dla sposobu rozumowania ucznia dowód procedury uzyskiwania rozwiązania równania liniowego
Dokonajmy w tym miejscu przeglądu wszystkich w szkolnej edukacji postaci równań liniowych:
Pokazanie uczniom w takiej hierarchicznej kolejności tych 20 postaci równań pozwala nauczycielowi na wstrzymanie prezentacji w każdym momencie procesu edukacji i wyćwiczenie poszczególnych typów nie tylko do poziomu biegłości, ale co istotniejsze, również do etapu zrozumienia. Jednocześnie pozwala to na uniknięcie metody aksjomatycznej – koszmaru każdego nauczyciela matematyki: „bo tak się postępuje w matematyce”, umożliwia bowiem przystępne wytłumaczenie uczniowi „dlaczego tak się robi”. Oczywiście omawiana procedura w tych dwudziestu 20 przypadkach była znana, lecz z uwagi na brak omówionego twierdzenia i kilka przypadków szczególnych, omawianych poniżej, autorzy podręczników szkolnych nie potrafili dotychczas pokazać, że i w tych pozostałych przypadkach omawiany algorytm również jest efektywny. Wymaga jedynie właściwej analizy. Dydaktyka rozwiązywania równań w szkolnej matematyce jest rozłożona na wiele lat ( program podstawowy nauczania matematyki w Polsce rozkłada zagadnienie rozwiązywania równań liniowych na 12 lat) – na różnych etapach edukacji, różni autorzy omawiają tylko część zagadnienia, właściwą dla danego programu podręcznika. To z kolei skutkuje u większości lękiem i zaniżoną samooceną nakazującą przekonanie, że zagadnienie jest trudne, podobnie jak cała matematyka. Jak widać z powyższego, taki sposób prezentacji zagadnienia pozwala nawet uczniowi o nikłych zdolnościach i kompetencjach matematycznych przyswoić i zrozumieć sposób rozwiązywania równań liniowych i to na bardzo wczesnym etapie edukacji matematycznej. Poniżej pokażemy cztery postaci równań liniowych, które wymagają jedynie analizy wystarczającej do posługiwania się omówioną twierdzeniem procedurą dwóch kroków:
W tym miejscu standardowo pojawia się pytanie uczniów: dlaczego od obydwu stron równania odejmujemy a? Wystarczy pokazać, że a – bx = c to skrócony zapis (transpozycja) równania: 0 + a – bx = c. Można również rozwiązać problem z punktu widzenia dydaktyki wprowadzając regułę porządkowania równania przed przystąpieniem do jego rozwiązywania. Reguła może wtedy przyjąć znane brzmienie: wielomiany porządkujemy od najwyższej do najniższe potęgi niewiadomej. W przypadku równań liniowych będziemy żądali aby tak uporządkować równanie , aby niewiadoma x była zapisana na początku równania. Postulowana procedura obowiązuje także w tych przypadkach.
22. ax + bx = c
W poprzednich przykładach zapisu postaci równania liniowego mieliśmy do czynienia z sytuacją jednokrotnego występowania w równaniu niewiadomej x. Wystarczy w tym miejscu przypomnienie uczniom pewnej intuicji:
5 = (2 + 3) = (1 + 4) = (7 – 2) etc. Obojętnie jakie obiekty porównujemy przez dodawanie i odejmowanie ( jabłka, znaczki, pieniądze, x) mamy:
2jabłka + 3 jabłka = (2 + 3)jabłka 2x + 3x = (2 + 3)x
Po upewnieniu się, że uczeń potrafi biegle i swobodnie posługiwać się tym narzędziem łatwo jest mu rozumieć transpozycję :
ax + bx = c <=> (a + b)x = c
i stosować omówioną powyżej, tak łatwą do przyswojenia procedurę dwóch kroków - zawsze prowadząca do sukcesu.
23. ax – c = bx + d
Jest to trzecia postać równania liniowego sprawiająca uczniom problem przyswojenia, a tym bardziej rozumienia rozwiązania równania liniowego: niewiadoma w równaniu nie tylko, że występuje więcej niż jeden raz, lecz na dodatek pojawia się po obydwu stronach równania. Pokazanie jak w 22, kilku transpozycji w rodzaju :
x = 3 |+x
x + x = x +3 <=> 2x = x + 3
2x = x + 3
pozwala uczniowi na takie uporządkowanie równania liniowego by dalej zastosować omówioną procedurę dwóch kroków, a samo rozwiązanie uczynić łatwym do wyćwiczenia i zrozumienia.
24. Ostatnią postacią zapisu równania liniowego sprawiającym najwięcej problemów zarówno dydaktyce tego zagadnienia, jak i praktyce szkolnej w relacji nauczyciel uczeń, jest postać wymierna (ułamkowa ) zapisu równania liniowego, która w najprostszym zapisie ma postać:
Uczniom, przy nieuporządkowanym hierarchicznie sposobie wprowadzania do dydaktyki problemu, nastręcza problemy zapamiętanie i zrozumienie dlaczego podręczniki proponują następujące operacje:
Problem łatwo rozwiązuje przypomnienie intuicji, że:
Przypomnienie uczniowi tej intuicji pozwala na dostrzeżenie, że nie jest to nawet transpozycja wyjściowego równania, a jedynie inny sposób jego zapisu, co pozwala na korzystanie z omawianej wyżej procedury dwóch kroków:
Czyni to także łatwym przekształcenia wzorów fizycznych mających taką właśnie postać równań liniowych:
Wielu ekspertów od dziesięcioleci postuluje konieczność radykalnych zmian w dydaktyce matematyki, tkwiącej we wzorcach, które wykrystalizowały tradycją szkolną i sposobem konstruowania podręczników do matematyki przed dwoma stuleciami a największe sukcesy święciły w społeczeństwie, które rządziło się zupełnie odrębnymi regułami od obowiązujących współcześnie. Efekt jest taki, że podręczniki kilkaset pojęć definiują w sposób zupełnie niezrozumiały, a nawet nielogiczny. Znawcom i ekspertom, z różnych zresztą dziedzin, to nie przeszkadza, np. w oprogramowaniu Microsoft, żeby wyłączyć komputer trzeba kursor naprowadzić na ikonę z napisem start – dziwi się tylko ktoś, kto pierwszy raz ma wykonać tę procedurę. Podobnie jest z nauczaniem matematyki. Tą szkolną trzeba po prostu napisać od nowa .
